Разбор квалификационного раунда Яндекс.Алгоритм 2017
Этот раунд был подготовлен разработчиками минского офиса Яндекса.
Задача А. Управление задачами
Рассмотрим решение, которое работает с квадратичной асимптотикой. Для этого будем действовать в соответствии с условием задачи: заведем счетчик последней закрытой задачи, будем проходить по списку задач от начала до конца, увеличивая счетчик, когда проходим через элемент массива задач, соответствующий следующей задаче. Из-за достаточно больших ограничений это решение не укладывается по времени.
Рассмотрим, в каком случае, мы уже не найдем никакой подходящей задачи до конца списка. Оказывается, только в том случае, когда после закрытия задачи с номером x следующая задача с номером (x+1) расположена ближе к началу списка. Следовательно, для решения задачи нужно по каждому номеру задачи узнать ее позицию в списке задач, а затем подсчитать количество различных номеров x таких, что позиция задачи с номером (x+1) меньше, чем позиция задачи с номером x.
К найденному количеству нужно добавить первый проход по списку задач. Итоговая трудоемкость алгоритма 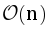 .
.
Задача B. Междугороднее общение
Задача “Междугороднее общение” не содержит особой алгоритмической идеи, поэтому нужно аккуратно реализовать описанное в условии задачи поведение системы бронирования.
Мы можем зафиксировать число от 0 до 23 (час, в который будем проверять возможность организации встречи). После этого в каждом из городов нужно проверить наличие свободной переговорки.
Отметим, что при больших ограничениях сохранить свободную переговорку для каждой пары (город, час) следовало бы до обработки запросов. Это позволило бы всегда отвечать на запрос за время пропорциональное количеству городов, а не суммарному количеству переговорок.
Задача C. Запуск тестов
Для этой задачи можно придумать несколько различных подходов к решению задачи, рассмотрим два из них.
Первое решение основано на подсчете количества раз, сколько раз тест с номером x будет запущен. В исходной системе каждой тест запускается один раз, а в новой системе 2d(x), где d(x) расстояние от корневого тест до теста с номером x. Это утверждение несложно доказывается методом математический индукции, также заметить этот факт можно было внимательно изучив описание тестовых примеров из условия. Для подсчете d(x) достаточно обойти дерево любым обходом.
Второй метод решения основан на динамическом программировании. Пусть T(x) равно суммарному времени работы теста с номером x, т.е. времени работы тестов, от которых он зависит, и времени проверки ax. Запишем соотношение:
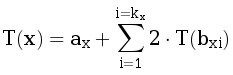
Для вычисления ответа T(1) также достаточно одного обхода дерева (в данном случае DFS).
Трудоемкость решения задачи 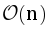 .
.
Задача D. Среднее арифметическое кодирование
Сразу следует рассмотреть такую задачу: на какое количество слагаемых можно разбить число n, если все слагаемые должны быть степенями двойки с целыми неотрицательными степенями. Покажем, что для любого целого k от popcount(n) до n это возможно (где popcount(n) это количество установленных бит в двоичной записи n).
Очевидно, что нельзя использовать меньшее чем popcount(n) число слагаемых, и большее n. Если у нас есть разложение в x слагаемых (x < n), то среди них есть слагаемое 2t с положительной степенью t. Его мы можем заменить на два слагаемых 2t-1, получив разложение с (x+1) слагаемым. Разложение из popcount(n) слагаемых строится из двоичного представления числа.
Для решения задачи будет перебирать длину последовательности k (k ≥ 1), пока не найдем подходящее. Как показано выше, нужно найти минимальное k, что popcount(kn) ≤ k, а после этого построить требуемое разложение. Для ограничений задачи k не превосходит 60 (60 ⋅ (250 - 1) < 260 - 1 = 20 + 21 + … + 259).
Задача E. Соединение серверов
Требуется чтобы в графе соединений не было мостов, следовательно степень всех вершин не менее двух. А так как сумма степеней всех вершин равна 2 ⋅ n + 2, то у нас возможны два случая:
- есть одна вершина степени 4;
- есть две вершины степени 3.
Рассмотрим первый случай. Граф представляет собой объединение двух циклов длины (m + 1) и (n - m) с общей вершиной. В этом случае нам нужно выбрать какие вершины попадут в первый цикл (остальные попадут во второй), и в каком порядке вершины окажутся на этих циклах. Общая формула имеет следующий вид
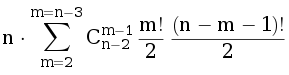
Рассмотрим второй случай. В графе есть две вершины степени три, которые соединены между собой цепочками ребер, на которых расположены все остальные (n-2) вершины. Сразу обратим внимание, что соединение с нулем дополнительных вершин (ребро) может быть только одно. Пусть на соединениях расположены a, b и c вершины (a ≤ b ≤ c). Рассмотрим несколько случаев:
- 0 ≤ a < b < c, тогда количество соединений равно
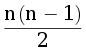
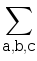 C(n-2, a) C(n - 2 - a, b)
C(n-2, a) C(n - 2 - a, b) 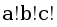 ;
; - 0 < a = b < c, тогда количество соединений равно
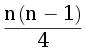
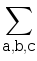 C(n-2, a) C(n - 2 - a, b)
C(n-2, a) C(n - 2 - a, b) 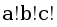 ;
; - 0 ≤ a < b = c, тогда количество соединений равно
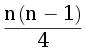
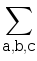 C(n-2, a) C(n - 2 - a, b)
C(n-2, a) C(n - 2 - a, b) 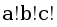 ;
; - 0 < a = b = c, тогда количество соединений равно
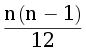
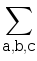 C(n-2, a) C(n - 2 - a, b)
C(n-2, a) C(n - 2 - a, b) 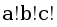 .
.
Собирая все формулы вместе, получаем итоговый результат.
Задача F. Повторения
Для решения этой задачи обратимся к строковой терминологии. Бордером строки s называется какая строка y, что x начинается и заканчивается на y.
Тогда в задаче нам для каждого префикса исходного текста нужно найти максимальный по длине бордер, которых имеет еще хотя бы одно дополнительное вхождение. Для этого можно найти все бордеры префикса, и в порядке убывания длин найти найти первый, который имеет дополнительное вхождение.
Для поиска всех бордеров можно использовать префикс-функцию. Дополнительно вспомнив, что 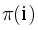 — длина максимального бордера, а длины всех бордеров префикса длины i можно перечислить, пройдя по последовательности
— длина максимального бордера, а длины всех бордеров префикса длины i можно перечислить, пройдя по последовательности 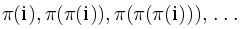 и т.д.
и т.д.
Следующий интересный факт: у бордера длины 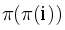 всегда есть не менее трех вхождений: первое начинается в начале строки, второе заканчивает в позиции i, а третье заканчивается в позиции
всегда есть не менее трех вхождений: первое начинается в начале строки, второе заканчивает в позиции i, а третье заканчивается в позиции 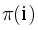 .
.
Следовательно, для полного решения задачи нам осталось научиться проверять, есть ли дополнительное вхождение максимального по длине бордера (длины 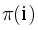 ). Чтобы такое вхождение было, должна найтись позиция j (j < i), в которой
). Чтобы такое вхождение было, должна найтись позиция j (j < i), в которой 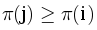 . Для быстрой проверки такого неравенства достаточно хранить префиксный максимум значений префикс-функции.
. Для быстрой проверки такого неравенства достаточно хранить префиксный максимум значений префикс-функции.
Трудоемкость решения задачи линейная от длины текста.