Разбор разогревочного раунда
Задачи раунда были подобраны Олегом Христенко aka snarknews.
Задача A. Арифметическая задача
В данной задаче требовалось написать ровно то, что требуется в условии — начать перебирать целые числа, начиная с единицы, дойти до первого числа, которое не делит n, и вывести его. Несмотря на то, что само n достаточно больше, это работает быстро, так как в ограничениях задачи ответ всегда не превосходит 22 (наименьшее общее кратное всех целых чисел от 1 до 23 это 5354228880, что уже превосходит максимально возможное значение n).
Это была одна из самых простых задач контеста, в которой, тем не менее, многие участники по причине спешки на первых минутах контеста получали WA 4 из-за того, что машинально перебирали ответ не от 1 до бесконечности, а от 1 до n, что, конечно же, не работает при n = 1 и n = 2. Особенно, наверное, обидно допустить такой баг, отправив задачу втёмную :)
n = int(raw_input())
for i in xrange(1, n + 2):
if n % i != 0:
print i
break Задача B. Построение четырёхугольника
Наряду с задачей А данная задача была одной из самых лёгких. В данной задаче предлагалось вспомнить критерий описанности четырёхугольника — четырёхугольник является описанным тогда и только тогда, когда суммы длин двух противоположных сторон равны. Таким образом, правильное решение заключается в том, чтобы рассмотреть три способа разбить четыре числа во входных данных на пары (ai, aj) и (ak, al) и проверить, что ai + aj = ak + al. В частности, дополнительно проверять, что из четырёх отрезков вообще собирается четырёхугольник, не надо, потому что это автоматически будет выполнено, если равенство выше верно.
a, b, c, d = map(int, raw_input().split())
if a + b == c + d or a + c == b + d or a + d == b + c:
print "Yes"
else:
print "No"Задача C. Циклопы и линзы
Данную задачу можно решить с помощью какого-либо жадного соображения. Будем говорить, что циклопы спарены, если они носят линзы из одной пары. Очевидно, мы хотим максимизировать количество спаренных циклопов.
Рассмотрим циклопа с минимальным li, пусть это значение равно x. Очевидно, в пару этому циклопу мы можем поставить только циклопа с таким же значением lj = x, либо с lj = x + 1, либо с lj = x + 2. Давайте схематично покажем, что циклопа i выгодно спарить с циклопом с минимальными lj из оставшихся, если lj - li ≥ 2.
Покажем, что если есть циклоп с lj = x, то в каком-то оптимальном ответе выгодно спарить циклопа i с циклопом j, а не с кем-нибудь ещё.
Если циклоп i не спарен ни с кем, то просто поставим циклопа j в пару к нему, таким образом мы либо одну пару циклопов потеряем (если j находился в паре с кем-то), а пару (i, j) образуем, либо же мы спарим двух неспаренных циклопов (если j был тоже одинок). Видно, что это не ухудшает ситуацию.
Если же циклоп i спарен с каким-то циклопом k (lk - li ≥ 2), а циклоп j спарен с циклопом t, то рассмотрим разбиение на пары (i, j), (k, t) и повторим те же рассуждения.
Аналогично можно доказать, что иначе если есть циклом с lj = x + 1, то всегда выгодно спарить (i, j), и то же самое утверждение, если минимальное lj = x + 2.
Таким образом, мы получили простой жадный алгоритм (гораздо более простой, чем его строгое обоснование!): мы идём по циклопам в порядке возрастания li и пытаемся спарить каждого очередного циклопа со следующим, если это возможно. Если не получилось, покупаем пару линз только на текущего и переходим к следующему циклопу, иначе покупаем на них одну пару линз на двоих, и переходим дальше. Данное решение работает за время сортировки последовательности входных данных.
n = int(raw_input())
A = map(int, raw_input().split())
A = sorted(A)
i = 0
ans = 0
while i < n:
if i + 1 < n and A[i + 1] - A[i] <= 2:
ans += 1
i += 2
else:
ans += 1
i += 1
print ansЗадача D. Два преобразования
Во-первых, оставим от каждого числа во входных данных только его остаток от деления на 2. Отдельно разберём случай n = 1, который не доставляет особых трудностей.
Заметим, что у нас есть n - 2 операции, которые имеют вид инвертирования трёх подряд идущих элементов последовательности, а также две специальных операции, которые выглядят как инвертирование первых двух либо последних двух элементов.
Очевидно, порядок применения операций не имеет значения, а значит, каждую операцию мы применим не более, чем один раз. Пусть мы, для определённости, делаем все числа чётными, то есть, нулями. Переберём два варианта: либо мы будем использовать инвертирование двух первых элементов, либо нет. Если мы решили использовать, инвертируем их.
Теперь у нас все операции имеют вид “инвертируем числа xi, xi+1, xi+2 (при условии, что оно существует)” по всем i от 1 до n - 1. Заметим, что теперь однозначно определяется, надо ли использовать каждую следующую операцию: действительно, если x1 = 1, то мы точно будем использовать первую операцию, иначе точно не будем. Инвертируем x1, x2, x3, потом, глядя на x2 мы однозначно понимаем, надо ли использовать вторую операцию, и так далее.
Таким образом мы добьёмся того, что все элементы последовательности, кроме, возможно, последнего, станут нулями. Если последний не стал единицей, значит зафиксированный нами вариант использования операции над x1 и x2 был неудачным, и в нём вообще невозможно добиться требуемого. Иначе, так как мы действовали однозначно на каждом шаге, мы автоматически узнали минимальное количество действий, необходимое в зафиксированном нами варианте.
Найдём общий ответ как минимум из ответов для двух вариантов того, используем ли мы операцию над x1 и x2 в начале, или нет.
Аналогично поступим, чтобы сделать все числа нечётными. Сложность полученного решения — O(n).
#include <cstdio>
#include <algorithm>
#include <memory.h>
using namespace std;
const int N = 1000500;
int A[N];
int B[N];
int n;
void inv(int x) {
for (int y = x - 1; y <= x + 1; y++) {
if (y >= 0 && y < n)
A[y] ^= 1;
}
}
int go(int a, int b) {
memcpy(A, B, sizeof(A));
int cnt = 0;
if (a) {
inv(0);
cnt++;
}
for (int i = 0; i < n - 1; i++) {
if (A[i] != b) {
cnt++;
inv(i + 1);
}
}
if (A[n - 1] != b)
return N;
else
return cnt;
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &B[i]);
B[i] &= 1;
}
int o = min(go(0, 1), go(1, 1));
int e = min(go(0, 0), go(1, 0));
if (o == N)
o = -1;
if (e == N)
e = -1;
printf("%d\n%d\n", o, e);
}Задача E. Точки и окружности
У данной задачи есть два подхода к решению. Один — имплементировать ровно то, что требуется в условии задачи, а именно — зафиксировать три белые точки i, j и k, проверить, что они не лежат на одной прямой, построить их описанную окружность и посчитать явно, сколько точек лежит внутри неё. Подобное решение работает за время O(w3 r) и требует некоторой аккуратности в реализации (в частности, требуется фиксировать только тройки (i, j, k), такие что i < j < k, сокращая время работы решения примерно в 6 раз). Ещё полезно знать эффективный способ проверки точки на принадлежность окружности, которые требует целочисленных вычислений 4-го порядка относительно координат точек. Можно показать, что точка p = (px, py) лежит внутри окружности, описанной около точек a = (ax, ay), b = (bx, by), c = (cx, cy), тогда и только тогда, когда знак определителя
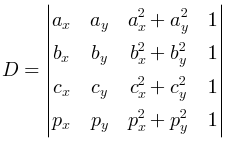
совпадает со знаком минора
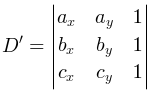
У этого факта, кстати, есть очень забавная геометрическая интерпретация: рассмотрим параболоид z = x2 + y2 в трёхмерном пространстве. Поднимем точки a, b, c и p на этот параболоид, получим четыре трёхмерных точки 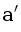 ,
, 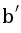 ,
, 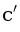 и
и 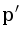 . Оказывается, точка p лежит внутри окружности, описанной около a, b и c, тогда и только тогда, когда
. Оказывается, точка p лежит внутри окружности, описанной около a, b и c, тогда и только тогда, когда 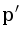 находится под плоскостью, проходящей через
находится под плоскостью, проходящей через 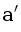 ,
, 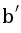 и
и 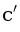 . Это условие является линейным, и выполняется в зависимости от знака определителя D, который задаёт ориентацию тетраэдра
. Это условие является линейным, и выполняется в зависимости от знака определителя D, который задаёт ориентацию тетраэдра 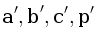 .
.
Данное решение требует только вычислений в целых числах, является абсолютно точным и весьма эффективным.
Данная задача также допускает решение за время 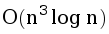 , использующее преобразование геометрической инверсии, но его мы подробно разбирать не будем, так как оно работает примерно столько же, сколько и решение за четвёртую степень. Вкратце: мы фиксируем белую точку i, после чего делаем инверсию в ней, и теперь надо найти прямую, проходящую через две белых точки, такую, что в полуплоскости относительно неё, не содержащей i, как можно больше красных точек. Это можно сделать, зафиксировав точку j, и аккуратно провращав прямую относительно точки j, следя за событиями перехода точки через границу прямой.
, использующее преобразование геометрической инверсии, но его мы подробно разбирать не будем, так как оно работает примерно столько же, сколько и решение за четвёртую степень. Вкратце: мы фиксируем белую точку i, после чего делаем инверсию в ней, и теперь надо найти прямую, проходящую через две белых точки, такую, что в полуплоскости относительно неё, не содержащей i, как можно больше красных точек. Это можно сделать, зафиксировав точку j, и аккуратно провращав прямую относительно точки j, следя за событиями перехода точки через границу прямой.
#include <cstdio>
#include <cassert>
using namespace std;
const int N = 200;
const int MAX = 10 * 1000;
int AX[N], AY[N], S[N];
int BX[N], BY[N], T[N];
typedef long long llong;
int main(int argc, char* argv[]) {
int w, r;
scanf("%d", &w);
for (int i = 0; i < w; i++) {
scanf("%d %d", &AX[i], &AY[i]);
S[i] = AX[i] * AX[i] + AY[i] * AY[i];
}
scanf("%d", &r);
for (int i = 0; i < r; i++) {
scanf("%d %d", &BX[i], &BY[i]);
T[i] = BX[i] * BX[i] + BY[i] * BY[i];
}
if (BX[1] == 101) {
puts("1");
return 0;
}
int ans = 0;
for (int i = 0; i < w; i++) {
for (int j = 0; j < i; j++) {
for (int k = 0; k < j; k++) {
llong d4 = (AX[i] * AY[j] * (llong)S[k] + AX[j] * AY[k] * (llong)S[i] + AX[k] * AY[i] * (llong)S[j]) -
(AX[i] * AY[k] * (llong)S[j] + AX[j] * AY[i] * (llong)S[k] + AX[k] * AY[j] * (llong)S[i]);
llong d3 = (AX[i] * AY[j] * 1 + AX[j] * AY[k] * 1 + AX[k] * AY[i] * 1) -
(AX[i] * AY[k] * 1 + AX[j] * AY[i] * 1 + AX[k] * AY[j] * 1);
llong d2 = (AX[i] * 1 * (llong)S[k] + AX[j] * 1 * (llong)S[i] + AX[k] * 1 * (llong)S[j]) -
(AX[i] * 1 * (llong)S[j] + AX[j] * 1 * (llong)S[k] + AX[k] * 1 * (llong)S[i]);
d2 = -d2;
llong d1 = (1 * AY[j] * (llong)S[k] + 1 * AY[k] * (llong)S[i] + 1 * AY[i] * (llong)S[j]) -
(1 * AY[k] * (llong)S[j] + 1 * AY[i] * (llong)S[k] + 1 * AY[j] * (llong)S[i]);
if (d3 == 0)
continue;
int cnt = 0;
for (int t = 0; t < r; t++) {
llong det = BX[t] * d1 - BY[t] * d2 + T[t] * d3 - d4;
cnt += (det < 0) == (d3 > 0);
}
if (ans < cnt)
ans = cnt;
}
}
}
printf("%d\n", ans);
}#include <cstdio>
#include <cassert>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
const double pi = acos(-1.0);
struct vt {
double x = 0, y = 0;
vt(double _x, double _y) {
x = _x, y = _y;
}
friend vt operator -(vt a, vt b) {
return vt(a.x - b.x, a.y - b.y);
}
friend vt operator +(vt a, vt b) {
return vt(a.x + b.x, a.y + b.y);
}
friend double operator *(vt a, vt b) {
return a.x * b.x + a.y * b.y;
}
friend double operator ^(vt a, vt b) {
return a.x * b.y - b.x * a.y;
}
friend vt operator *(vt a, double k) {
return vt(a.x * k, a.y * k);
}
friend vt operator *(double k, vt a) {
return vt(a.x * k, a.y * k);
}
friend vt operator /(vt a, double k) {
return vt(a.x / k, a.y / k);
}
double sqabs() {
return x * x + y * y;
}
double ang() {
return atan2(y, x);
}
vt() {}
};
vector<vt> W;
vector<vt> R;
vector<vt> A, B;
struct evt {
double ang;
int delta = 0;
evt(double _ang, int _delta)
: ang(_ang), delta(_delta)
{}
friend bool operator <(const evt& a, const evt& b) {
return a.ang < b.ang;
}
};
const double eps = 1e-9;
vector<evt> E;
int main() {
int w, r;
scanf("%d", &w);
double u = cos(0.042), v = sin(0.042);
//u = 1, v = 0;
for (int i = 0; i < w; i++) {
double x, y;
scanf("%lf %lf", &x, &y);
x = u * x + v * y;
y = -v * x + u * y;
W.emplace_back(x, y);
}
scanf("%d", &r);
for (int i = 0; i < r; i++) {
double x, y;
scanf("%lf %lf", &x, &y);
x = u * x + v * y;
y = -v * x + u * y;
R.emplace_back(x, y);
}
int ans = 0;
for (int i = 0; i < w; i++) {
A.clear();
B.clear();
for (int j = 0; j < w; j++) {
if (j != i)
A.emplace_back((W[j] - W[i]) / (W[j] - W[i]).sqabs());
}
for (int j = 0; j < r; j++) {
B.emplace_back((R[j] - W[i]) / (R[j] - W[i]).sqabs());
}
for (int j = 0; j < (int)A.size(); j++) {
E.clear();
for (int k = 0; k < (int)B.size(); k++) {
double ang1 = ((B[k] - A[j])).ang();
double ang2 = ang1 + pi;
if (ang2 > pi)
ang2 -= 2 * pi;
evt e1(ang1, -1);
evt e2(ang2, 1);
E.emplace_back(e1);
E.emplace_back(e2);
}
for (int k = 0; k < (int)A.size(); k++) {
if (k != j) {
double ang1 = ((A[k] - A[j])).ang();
double ang2 = ang1 + pi;
if (ang2 > pi)
ang2 -= 2 * pi;
evt e1(ang1, 0);
evt e2(ang2, 0);
E.emplace_back(e1);
E.emplace_back(e2);
}
}
{
double ang1 = (vt(0, 0) - A[j]).ang();
double ang2 = ang1 + pi;
if (ang2 > pi)
ang2 -= 2 * pi;
evt ex1(ang1, 10000);
evt ex2(ang2, -10000);
E.emplace_back(ex1);
E.emplace_back(ex2);
}
stable_sort(E.begin(), E.end());
int cur = 0;
for (int k = 0; k < (int)B.size(); k++) {
if (B[k].y < A[j].y)
cur++;
}
if (A[j].y > 0)
cur -= 10000;
int _cur = cur;
for (int k = 0; k < (int)E.size(); k++) {
cur += E[k].delta;
if (E[k].delta == 0) {
ans = max(ans, cur);
}
}
assert(_cur == cur);
}
}
printf("%d\n", ans);
}Задача F. Обслуживание сети
Данная задача сводится к задаче нахождения потока минимальной стоимости.
Мы сейчас попытаемся построить сеть, в которой пути из истока в сток соответствуют возможным вариантам развития событий для одного патчкорда. Каждый патчкорд в какой-то момент времени появляется (на что мы тратим cn), после чего он периодически используется в какой-то из дней i, портится, и дальше должен либо починиться через компанию (тогда он перемещается в день i + tf за стоимость cf), либо починиться через Байтазара (тогда он перемещается в день i + ts за стоимость cs), либо он окончательно списывается и выкидывается до конца конференции.
Давайте это интерпретировать следующим образом: рассмотрим сеть, в которой есть исток s, сток t, а также n пар вершин (1+, 1-), (2+, 2-), … (n+, n-), соответствующих дням конференции. Зачем каждому дню сопоставлять две вершины будет объяснено отдельно.
Скажем, что из истока s в вершину i- входит ребро стоимости cn и пропускной способности 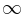 . Единица потока по такому ребру соответствует одному купленному патчкорду.
. Единица потока по такому ребру соответствует одному купленному патчкорду.
Скажем, что из вершины i+ в вершину i- ведёт ребро пропускной способности ri и стоимости -A, где A — некоторая положительная величина. Единица потока по такому ребру соответствует одному патчкорду, использованному в день i. Назовём рёбра такого вида важными.
Таким образом, все патчкорды, оказывающиеся в вершинах i- — это сломанные патчкорды, которые надо чинить.
Скажем, что из вершины i- исходит ребро пропускной способности 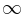 и стоимости 0 в t. Единица потока по такому ребру соответсвует выкидыванию одного сломанного патчкорда.
и стоимости 0 в t. Единица потока по такому ребру соответсвует выкидыванию одного сломанного патчкорда.
Скажем, что из вершины i- исходит ребро пропускной способности 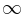 и стоимости cf в (i+tf)+. Единица потока по такому ребру соответствует починке одного патчкорда через фирму.
и стоимости cf в (i+tf)+. Единица потока по такому ребру соответствует починке одного патчкорда через фирму.
Скажем, что из вершины i- анаологичнымбразом исходит ребро пропускной способности 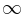 и стоимости cs в (i+ts)+. Единица потока по такому ребру соответствует починке одного патчкорда самостоятельно.
и стоимости cs в (i+ts)+. Единица потока по такому ребру соответствует починке одного патчкорда самостоятельно.
Наконец, скажем, что из вершины i+ исходит ребро пропускной способности 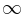 и стоимости 0 в (i+1)+. Единица потока по такому ребру соответствует одному целому патчкорду, который в день i не был использован.
и стоимости 0 в (i+1)+. Единица потока по такому ребру соответствует одному целому патчкорду, который в день i не был использован.

Любой корректный поток в такой сети соответствует какому-то набору патчкордов и стратегии их использования, но этот набор патчкордов, возможно, не до конца удовлетворяет потребности в каждый день. Нас интересуют только такие потоки, которые насыщают все важные рёбра. Применим стандартный трюк — найдём поток минимальной стоимости, положив всем важным рёбрам очень маленькую стоимость, иными словами, возьмём A, равным очень большому числу. Тогда итоговая стоимость потока будет равна -A ⋅ satcnt + opcost, где satcnt — количество насыщенных важных рёбер, а opcost — стоимость покупки/починки всех использованных патчкордов.
Найдём поток минимальной стоимости (обратите внимание, он не обязательно является максимальным потоком в данной сети). Несложно видеть, что такой поток в первую очередь максимизирует количество насыщенных важных рёбер, то есть, достигает требования, что в каждый день нам хватает целых патчкордов, а во вторую минимизирует затраты на соответствующий план использования.
Таким образом, мы получили решение, работающее за время одного запуска алгоритма нахождения потока минимальной стоимости в сети без отрицательных циклов. Алгоритм нахождения кратчайшего увеличиавающего пути с помощью Форда-Беллмана работает без особых проблем при данных ограничениях.
#include <cstdio>
#include <algorithm>
#include <vector>
#include <cassert>
using namespace std;
const int N = 500;
const int M = 40000;
typedef long long llong;
struct edge
{
int t;
llong f, c, u;
int nxt;
} E[2 * M];
int first[N];
int ept = 0;
inline void add_edge(int a, int b, llong c, llong u)
{
assert(ept < 2 * M - 10);
E[ept] = {b, 0, c, u, first[a]};
E[ept + 1] = {a, 0, 0, -u, first[b]};
first[a] = ept;
first[b] = ept + 1;
ept += 2;
}
int prv[N];
llong D[N];
int S, T;
const llong inf = 1e12;
int n;
llong push()
{
for (int i = 0; i < n; i++)
D[i] = inf, prv[i] = -1;
D[S] = 0;
for (int i = 0; i < n; i++)
{
for (int e = 0; e < ept; e++)
{
if (E[e].f == E[e].c)
continue;
int a = E[e ^ 1].t;
int b = E[e].t;
if (D[a] + E[e].u < D[b])
D[b] = D[a] + E[e].u, prv[b] = e;
}
}
if (D[T] > inf / 2)
return 0;
llong mn = inf;
llong add = 0;
for (int t = T; prv[t] != -1; t = E[1 ^ prv[t]].t)
mn = min(mn, (llong)E[prv[t]].c - E[prv[t]].f);
assert(mn > 0);
for (int t = T; prv[t] != -1; t = E[1 ^ prv[t]].t)
E[prv[t]].f += mn, E[prv[t] ^ 1].f -= mn, add += E[prv[t]].u;
if (add >= 0) {
return 0;
}
return add * mn;
}
int R[N];
int main() {
int n;
double dcn, dcf, dcs;
int tf, ts;
scanf("%d %lf %lf %lf %d %d", &n, &dcn, &dcf, &dcs, &tf, &ts);
int cn = (int)(dcn * 100 + 0.5);
int cf = (int)(dcf * 100 + 0.5);
int cs = (int)(dcs * 100 + 0.5);
for (int i = 0; i < n; i++) {
scanf("%d", &R[i]);
}
int ver = 0;
vector<int> in(n);
vector<int> out(n);
int s = ver++;
int t = ver++;
S = s, T = t;
for (int i = 0; i < n; i++) {
in[i] = ver++;
out[i] = ver++;
}
::n = ver;
int sum = accumulate(R, R + n, 0);
for (int i = 0; i < n; i++) {
add_edge(in[i], out[i], R[i], -inf);
}
for (int i = 0; i < n; i++) {
add_edge(out[i], t, inf, 0);
add_edge(s, in[i], inf, cn);
}
for (int i = 0; i < n - 1; i++) {
add_edge(in[i], in[i + 1], inf, 0);
}
for (int i = 0; i + tf < n; i++) {
add_edge(out[i], in[i + tf], inf, cf);
}
for (int i = 0; i + ts < n; i++) {
add_edge(out[i], in[i + ts], inf, cs);
}
llong ans = 0;
while (llong p = push()) {
ans += p;
}
llong bot = sum * -inf;
assert(ans >= bot);
assert(ans < (sum - 1) * -inf);
ans -= bot;
printf("%lld.%02lld\n", ans / 100, ans % 100);
}