Разбор 1 тура

Краткий разбор первого тура.

Задача A.

Решение на 25.

Написать ровно то, что написано в условии. Если возникают проблемы с TL - предподсчитать gcd всех пар

Решение на 50. Первый способ.

Заметим, что решение на 25, отрабатывает минут за 10, на ограничениях этой подгруппы. Можно запустить решение локально, и послать программу, выводящую готовый ответ.

Решение на 50. Второй способ.

Для каждой пары, посчитаем их gcd. Соединим красным ребром пары, для которых gcd равен 1, и синим, пары для которых не равен 1. Тогда задача свелась к поиску одноцветных треугольников. Пусть у i-ой вершины x_i красных ребер и y_i синих. Количество разноцветных треугольников можно выразить через x_i, y_i. Конкретный способ выразить оставляется читателю.

Решение на 100.

Получается из решения на 50, более быстрым вычислением x_i, y_i. Можно доказать, что x_k выражается как сумма по некоторым делителям d числа k. Для вывода формулы следует применить принцип включений-исключений. Расстановка знаков в формуле, а также ее доказательство оставляется читателю.

Задача B.

В этой задаче возможно много разных решений. В конечном счете, они все сводятся к перебору каких-то параметров, позволяющих разбить фигуру на части. Например перебор можно организовать следующим образом.

Будем перебирать клетки по очереди сверху вниз, слева направо. В каждый момент у нас зафиксирована верхняя левая клетка каждой из полиоминошек, которые мы уже нашли. При рассмотрении очередной клетки она либо уже приписана к одной из полиоминошек, либо часть первой, либо верхняя левая клетка новой полиоминошки. Во втором и третьем случаях надо некоторые клетки приписать к некоторым полиоминошкам, пользуясь тем, что зафиксировав верхние левые клетки, мы знаем сдвиг.

Другое решение. Утверждается, что искомую фигуру можно получить как пересечение всей фигуры с ее сдвигом. Переберем все сдвиги и попытаемся замостить полученными фигурами.

Задача С.

Самая простая задача тура. Для полного решения, надо применить с конца операции, обратные к описанным. После этого понятно, где изначально была карта на позиции K.

Задача D.

Для решения первой подзадачи надо промоделировать процесс, описанный в условии задачи.

Для решения второй подзадачи надо было сделать тоже самое, либо достаточно аккуратно, либо ускорив подсчет суммы цифр в числе с помощью предподсчета.

Остальные подзадачи решаются динамикой. Заметим, что сумма цифр всегда небольшая. Рассмотрим момент, когда число первый раз имеет вид x*10^k + y (считаем, что k не очень маленькое). В таком случае y не превосходит суммы цифр в предыдущем числе, а значит 18 * 9.

Тогда можно сделать динамику по состоянию (сумма цифр в x, k, y) — количество ходов и y’ в первом числе вида 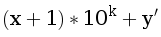. Склеивая такие переходы по 10, можно переходить к большим k. Ответ на задачу получается выбором наибольшей степени 10, которую можно прибавить не переполнив число ходов.

В зависимоcти от аккуратности решение будет получать от 70 до 100