Третий тур

RLE-буквы

Требовалось просто каким-нибудь способом визуализировать содержимое файла. Для маленьких картинок можно было просто вывести матрицу, для больших нужно было сжать ее, поделив большую матрицу на квадраты 100⋅100 и посчитав в каждом квадрате количество пикселей черного цвета. Далее вывести матрицу (h/100)⋅(w/100), где клетка черная, если в соответствующем квадрате не менее половины черных пикселей и белая иначе.

Дорожные работы.

После каждой операции нужно было проверить, что |E| = |V|-1 то есть, ребер в графе на одно меньше, чем вершин и граф связен. Проверку на связность можно делать dfs-ом, получается время работы O(nm)

Бинпоиск.

Пусть f(l,r) — минимальное время работы бинарного поиска на массиве {al, al+1, …, ar} Тогда понятно, что

f(l,r) = min s[m] + max(f(l,m-1), f(m+1, r)) : l ≤ m ≤ r
(будем считать, что ).

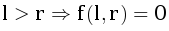То есть, мы перебираем, с каким элементом сравним в первую очередь и затем выбираем худший вариант ответа (максимум по ответам, среди половин).

Это наблюдение дает решение через дп по подотрезкам, работающее за O(n3), набиравшее 40 баллов

Теперь давайте отметим несколько фактов об f(l,r).

  1. f(l,r) ≤ f(l, r+1)
    Вообще это понятно интуитивно, но можно доказать индукцией по длине отрезка [l,r].
    База f(l,l) = 0, f(l,l+1) = max(s[l],s[l+1]) > 0
    Теперь рассмотрим m, на котором достигается минимум, при вычислении f(l,r+1).
    f(l,r+1) = s[m] + max(f(l,m-1), f(m+1,r+1)) ≥ s[m] + max(f(l,m-1), f(m+1,r)) ≥ f(l,r)
    (по индукционному предположению f(m+1,r+1) ≥ f(m+1,r) и f(l,r) — минимум по всем значениям m)

  2. Аналогично f(l,r) ≤ f(l-1,r)

Давайте, для начала, предположим, что s[x] = 1 для всех x.
Тогда f(l,r) = 1 + min { max(f(l,m-1),f(m+1,r)) }
f(l,m-1) возрастает c увеличением m, f(m+1,r) убывает с увеличением m
тогда max(f(l,m-1), f(m+1,r)) сначала убывает, затем возрастает (нестрого).

Тогда оптимальное значение max(f(l, m-1), f(m+1,r)) можно найти с помощью бинарного поиска.

Теперь вспомним, что значения s[x] различны (однако, в массиве не более трех различных чисел).
Тогда нам достаточно сделать три бинпоиска:
1. по таким m, что s[m] = a,
2. по таким m, что s[m] = b,
3. по таким m, что s[m] = c.

Получилось решение за O(n2 log n), которое должно было набирать 60 баллов.

Осталось сделать еще одно простое наблюдение, чтобы избавиться от логарифма.

Обозначим за g(l,r,k) оптимальный ответ, если первым разделителем выбирать m, такое, что s[m] = k и p(l,r,k) — наименьший оптимальный m, такой что s[m] = k. теперь заметим, что p(l,r,k) ≤ p(l, r+1, k) Это легко понять, нарисовав графики функций f(l,m-1), f(m+1,r) и f(m+1,r+1).

Но давайте докажем формально
пусть p(l,r,k) = m1, p(l,r+1,k) = m2
Пусть m1 > m2
f(l,m1-1) ≥ f(l, m2-1)
max(f(l,m1-1), f(m1+1,r+1)) ≥ max(f(l,m2-1), f(m2+1,r+1))
f(m1+1,r+1) ≤ f(m2+1,r+1)

если max(f(l,m2-1), f(m2+1,r+1)) = f(m2+1,r+1), то
f(l,m1-1) ≥ f(m1+1,r+1) ≥ f(m1+1,r)
иначе f(l,m2-1) ≥ f(m2+1,r+1) 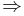т.к. m1>m2 f(l,m1-1) ≥ f(m1+1,r+1) ≥ f(m1+1,r)

m1 находится на промежутке возрастания функции max(f(l,m-1), f(m+1,r)) Так как он наименьший из оптимальных, m2 находится на промежутке убывания функции. То есть, f(l,m2-1) ≤ f(m2+1, r)
в свою очередь f(m2+1,r) ≤ f(m2+1,r+1)

g(l,r+1,k) = f(m2+1,r+1) + s[m2]
g(l,r,k) = f(l, m1-1) + s[m1]
f(m2+1,r) ≥ f(l,m1-1) (m1 оптимально)
тогда g(l,r+1,k) ≤ g(l,r,k), так как обратное неравенство тоже верно,
то g(l,r,k) = g(l,r+1,k), но тогда max(f(l,m2-1), f(m2+1,r)) ≤ max(f(l,m1-1), f(m1+1,r))
тогда m1 – не наименьший оптимальный средний элемент! противоречие.

Теперь поймем, что мы можем легко проверить, что значение m является оптимумом (для m+1 и m-1 ответы не лучше) Тогда можно фиксировать l, двигать r вправо и p(l,r,k) для каждого из трех возможных k тоже будет двигаться вправо.

Получили асимптотику O(n^2) и 100 баллов.

!! Если в похожей задаче не получается проверять, что m оптимум, но выполнено p(l, r-1) ≤ p(l,r) ≤ p(l+1,r), можно вместе с динамикой поддерживать p и искать оптимум только там, где нужно. Асимптотика при этом всё равно будет O(n2).

Выборы.

Чтобы максимизировать число мест в парламенте, нужно отдать все голоса нужной партии и промоделировать процесс раздачи мест.

Для минимизации нужно немного переформулировать алгоритм раздачи мест: Если партии получили v1, ..., vn голосов и 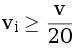, то сортируются пары вида (i – номер партии, j меняется от 1 до m)

…

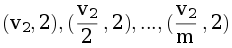
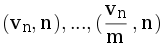
Пары сортируются по убыванию первого и по возрастанию второго значения.

Далее для первых m пар в списке соответствующие партии получают места в парламенте

Тогда, пусть партия k получила ≤ x мест в парламенте. Тогда в списке пар есть хотя бы m таких, что .

Тогда бинпоиском зафиксируем значение x, и посчитаем dp[i][j] — минимальное необходимое количество голосов, чтобы у первых i партий было суммарно j активных пар 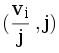больших . Тогда, если dp[n][m] ≤ числа свободных головов, то партия может получить ≤ x мест в парламенте.

Переход — чтобы партия i породила z пар, расположенных раньше , нужно, чтобы 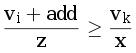(иногда ≥ иногда >)

Получилось решение за O(n log m * n * m2)

Можно рассматривать только партии, которые набрали не менее 5% голосов изначально (таких всего 20). Тогда можно считать n ≤ 20.