Четвертый тур
Задача А: Таможенные пошлины
Сразу хочется написать какую-нибудь динамику. Например, такую dp[i][j] — какое минимальное количество денег нужно заплатить, чтобы попасть из города i в город B, если у таможенников осталось j возможностей взять пошлину. dp[v][0] = 0 для всех v.
Решение за O(KVE)
Как можно было бы строить переходы. dp[i][j] = min { max { w[e] + dp[to][j-1], dp[to][j] } }, где e — ребро из i в to, w[e] — вес этого ребра. Действительно, если выбирать ребро e, то таможенники выбирают наиболее удачный для себя вариант, а нам нужно из всех вариантов перехода выбрать максимальный. Проблема только в том, что переходы цикличны.
От циклов в переходах можно избавляться многими способами. Самый простой — добавить в состояние длину пути в ребрах. dp[i][j][k] — какое минимальное количество денег нужно заплатить, чтобы попасть из города i в город B, путем, содержащим ровно k ребер, dp[i][j][k] = min { max { w[e] + dp[to][j-1][k-1], dp[to][j][k-1] } }. Тогда ответ — это максимум из dp[A][K][k] по всем k (K — количество пошлин, которое могут взять таможенники).
Такой подход дает решение за O(KVE) и 60 баллов.
Решение за 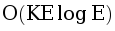
В первом случае мы пользовались подходом из алгоритма Форда-Беллмана, давайте воспользуемся принципом алгоритма Дейкстры. Будем рассматривать первый вариант динамики по слоям в порядке увеличения j. Будем поддерживать значения 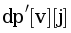 — минимальное количество денег, которое можно потратить, если ехать из города v только в города из множества S. При этом ,будем поддерживать инварианты
— минимальное количество денег, которое можно потратить, если ехать из города v только в города из множества S. При этом ,будем поддерживать инварианты 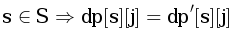 и
и 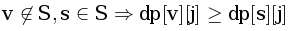 . Изначально положим S = {B} и будем, по аналогии с алгоритмом Дейкстры, добавлять в него по одной вершине, поддерживая инварианты. Изначально инвариант выполнен
. Изначально положим S = {B} и будем, по аналогии с алгоритмом Дейкстры, добавлять в него по одной вершине, поддерживая инварианты. Изначально инвариант выполнен 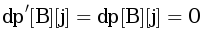 . Посчитаем остальные
. Посчитаем остальные  , для этого рассмотрим ребра, входящие в B, и выполним
, для этого рассмотрим ребра, входящие в B, и выполним 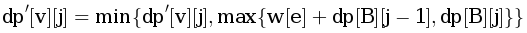 .
.
Рассмотрим множество U минимальных по значению dp[v][j] вершин из 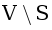 . Если хотя бы один оптимальный переход из U ведет в вершину S, то
. Если хотя бы один оптимальный переход из U ведет в вершину S, то  и можно добавлять u в S. Иначе переходы из вершин U содержат цикл (переход не может вести в вершину, строго большую по значению dp, получается, что в графе переходов |U| вершин и ребер).
и можно добавлять u в S. Иначе переходы из вершин U содержат цикл (переход не может вести в вершину, строго большую по значению dp, получается, что в графе переходов |U| вершин и ребер).
Если рассмотреть подробнее переходы, образующие цикл, то можно заметить, что dp[u][j-1] = dp[v][j-1] для любых u и v из этого цикла. Поэтому при переходах по этому циклу таможенники могут никогда не брать у нас пошлину (потому что dp[u1][j] = dp[u2][j-1] + w[e] = dp[u2][j], то есть, для таможенников никогда не хуже подождать с взятием пошлины). Тогда, когда мы выходим из этого цикла, мы переходим в вершину из S (так как j не меняется и вершины из 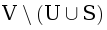 строго хуже по значению dp). Тогда существует вершина u ∈ U, такая, что
строго хуже по значению dp). Тогда существует вершина u ∈ U, такая, что  . Тогда можно, как и в алгоритме Дейкстры, каждый раз добавлять вершину с минимальным значением
. Тогда можно, как и в алгоритме Дейкстры, каждый раз добавлять вершину с минимальным значением  и обновлять значения в началах входящих в добавленную вершину ребер.
и обновлять значения в началах входящих в добавленную вершину ребер.
Задача B: Лифт
Не умаляя общности можем считать a ≤ b ≤ c. Также будем считать, что этажи нумеруются с нуля. Пусть p(i) = 1, если до этажа i можно доехать и 0 иначе. Очевидно, что 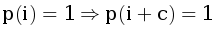 . Тогда давайте для всех k ∈ {0, …, c-1 } посчитаем минимальный этаж F(k), такой, что F(k) mod c = k и p(F(k)) = 1.
. Тогда давайте для всех k ∈ {0, …, c-1 } посчитаем минимальный этаж F(k), такой, что F(k) mod c = k и p(F(k)) = 1.
Рассмотрим некоторый остаток k. Тогда, если k+a < c, то F(k+a) ≤ F(k) + a. Если же k+a ≥ c, то F((k+a) mod (c)) ≤ F(k) + a. Аналогично можно прибавлять b. Построим граф G с вершинами {0, … c-1} и ребрами  и
и  . Второй элемент пары — длина соответствующего ребра. Тогда F(k) — длина кратчайшего пути из 0 в k в графе G.
. Второй элемент пары — длина соответствующего ребра. Тогда F(k) — длина кратчайшего пути из 0 в k в графе G.
С помощью F(k) легко посчитать ответ на задачу.
Кроме того, можно считать 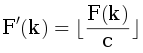 . F(k) легко выражается через
. F(k) легко выражается через 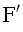 , а
, а 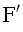 можно искать с помощью поиска в ширину по графу с весами ребер 0 и 1.
можно искать с помощью поиска в ширину по графу с весами ребер 0 и 1.
Задача C: Распределенные вычисления
Решение за O(n2)
Переберем пару серверов a и b. Множество точек, где сервер a становится ближайшим по x, а b — ближайшим по y — это прямоугольник. Точки из него, которые достаются серверу a лежат не ниже диагонали, проведенной из нижнего левого угла (если x растет слева-направо, а y снизу-вверх). Пусть прямоугольник имеет размеры w × h. Тогда оба количества легко посчитать: если w ≥ h, то серверу a достается  точек, если w < h, то серверу a достается
точек, если w < h, то серверу a достается  .
.
Решение за 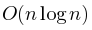
Рассмотрим сервер a и найдем количество точек для которых он станет ближайшим по иксу. Это полоса. Она поделится на прямоугольники, рассмотренные в предыдущем решении. Прямоугольники бывают двух типов: прямоугольники с w ≥ h и прямоугольники с w < h. Тогда нужно посчитать сумму  по всем первым и
по всем первым и  по вторым. Для этого нужно отсортировать горизонтальные полосы влияния серверов (полосы, где каждый сервер выбирается в качестве сервера y) по высоте и считать сумму на префиксе значений
по вторым. Для этого нужно отсортировать горизонтальные полосы влияния серверов (полосы, где каждый сервер выбирается в качестве сервера y) по высоте и считать сумму на префиксе значений  и сумму на суффиксе значений h. Таким образом, для каждого сервера мы выразили количество точек, которые достаются ему, если он выбирается в качестве сервера x.
и сумму на суффиксе значений h. Таким образом, для каждого сервера мы выразили количество точек, которые достаются ему, если он выбирается в качестве сервера x.
Аналогично можно посчитать количества точек, которые достаются каждому серверу, когда он выбирается в качестве сервера y.
Задача D: Подграф
Солнышко
Нужно найти любую вершину степени не меньше трех и взять ее и трех ее соседей.
Треугольник на палочке
Переберем вершину u степени не меньше 3, переберем ее соседа v и проверим, есть ли у u и v общий сосед. Проверять можно с помощью bitset’ов, получается время работы 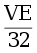 .
.
Цепочка
Переберем ребро (a,b), возьмем по три смежные вершины у a и b, если у них действительно есть по три смежных, то среди этих вершин найдется цепочка, длины 3.
Квадратик
Переберем две вершины a и b и найдем пересечение их списков смежности. Для этого пройдемся по всем вершинам смежным a и пометим в u[v] = (a,b) для всех v смежных a. Далее посмотрим на все вершины v смежные b и выберем такие, что u[v] = (a,b).
Квадратик с диагональю
Переберем ребро (оно будет диагональю) и пересечем множества смежности концов ребра с помощью bitset’ов. Если в пересечении есть хотя бы три вершины, то мы нашли нужный подграф.
Два ребра
Граф, где нет двух неинциндентных ребер — это либо треугольник, либо кисть. Иначе можно просто перебирать пару ребер и проверять, инциндентны ли они.