Разбор 2 тура
Задача A: Котята
В каждый момент времени можно поддерживать состояние каждого котенка, если котенок мяукнул, то это влияет на котят, слышащих его и спящих в данный момент. Никаких идей не требовалось
Задача B: Красим доски
Если K=1, то можно раскрасить только доску 1 × 1, если K=2, то возможна только шахматная раскраска.
Рассмотрим случай K=3. Пусть C1, C2, C3 — количества клеток, которые должны быть покрашены в первый, второй и третий цвет, соответственно. Будем считать C1 ≤ C2 ≤ C3. Если 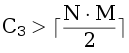 , то задача не имеет решения (на доске нет независимого множества клеток такого размера, максимальное независимое множество в двудольном графе имеет размер V - M, где V — количество вершин, M — размер максимального паросочетания).
, то задача не имеет решения (на доске нет независимого множества клеток такого размера, максимальное независимое множество в двудольном графе имеет размер V - M, где V — количество вершин, M — размер максимального паросочетания).
Построим раскраску в случае  . Будем считать, что N ≤ M.
. Будем считать, что N ≤ M.
Давайте выбросим какой-нибудь столбец доски и будем красить в первый цвет белые клетки, слева от него и черные клетки, справа от него. Остальные белые клетки покрасим во второй цвет, остальные черные — в третий.

Почему всё получится? Во-первых, места на первый цвет точно хватит,  , а клеток для третьего цвета будет
, а клеток для третьего цвета будет  . Если N ≥ 3, то понятно, что все хорошо, для N ∈ {1,2} можно проверить и понять, что всё тоже работает. Но количество клеток белого и черного цвета, которые нам нужно покрасить в первый цвет фиксировано (ведь все остальные белые клетки мы красим во второй, а все остальные черные — в третий цвет). Это тоже не проблема, мы всегда сможем выбрать хорошее положение вычеркнутого столбца.
. Если N ≥ 3, то понятно, что все хорошо, для N ∈ {1,2} можно проверить и понять, что всё тоже работает. Но количество клеток белого и черного цвета, которые нам нужно покрасить в первый цвет фиксировано (ведь все остальные белые клетки мы красим во второй, а все остальные черные — в третий цвет). Это тоже не проблема, мы всегда сможем выбрать хорошее положение вычеркнутого столбца.
Пусть C1 = C2 = C3 = 10, тогда доску 5 × 6 можно покрасить следующим образом:
- Покрасим клетки в первый цвет

- Теперь во второй и в третий

Как теперь решать задачу для K ≥ 3? Разобьем цвета на три группы так, чтобы в самой большой группе было в сумме не более 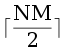 клеток. Будем действовать по следующему алгоритму: сначала в каждую группу положим один цвет, затем будет сливать две самые маленькие группы в одну, пока не получится три группы. Пусть есть G ≥ 4 групп. Суммарное количество клеток в самых маленьких
клеток. Будем действовать по следующему алгоритму: сначала в каждую группу положим один цвет, затем будет сливать две самые маленькие группы в одну, пока не получится три группы. Пусть есть G ≥ 4 групп. Суммарное количество клеток в самых маленьких 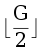 группах не превосходит
группах не превосходит 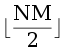 , две самые маленькие группы всегда входят в эту половину при G ≥ 4. Тогда в ходе алгоритма мы никогда не создадим группу размера больше
, две самые маленькие группы всегда входят в эту половину при G ≥ 4. Тогда в ходе алгоритма мы никогда не создадим группу размера больше 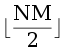 .
.
Задача C: Локальные максимумы
Давайте научимся проверять, может ли множество A быть множеством максимумов какой-нибудь перестановки.
Пусть множество является множеством максимумов перестановки p. Пусть  . Тогда давайте изображать разбиение {1, …, n} на A и B как строчу вида (i-й символ строчки равен A, если pi ∈ A, в противном случае i-й символ равен B, понятно, что два максимума не могут стоять рядом).
. Тогда давайте изображать разбиение {1, …, n} на A и B как строчу вида (i-й символ строчки равен A, если pi ∈ A, в противном случае i-й символ равен B, понятно, что два максимума не могут стоять рядом).
Тогда давайте выберем из каждого отрезка подряд идущих элементов B минимум, а остальные поставим в правый край перестановки. Понятно, что при этом множество максимумов новой перестановки будет содержать A. Чтобы оно было равно A, часть перестановки, правее последнего A нужно упорядочить по возрастанию. Тогда разбиение примет вид .
A = {a1, …, ak}; a1 ≤ a2 ≤ … ≤ ak. B = {b1, …, bq}; b1 ≤ b2 ≤ … ≤ bq; q+k = n.
a1 стоит между элементами bi, bj, то есть a1 ≥ bi, bj. Тогда a2 ≥ bi, bj кроме того, a2 стоит между элементами 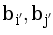 и
и 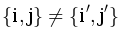 , то есть, не умаляя общности
, то есть, не умаляя общности 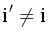 и
и 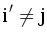 . Тогда
. Тогда  . Продолжая рассуждать аналогичным образом ap+1 ≥ bi1, bi2, … bip. Тогда перестановка с таким множеством максимумов может выглядеть как (b1, a1, b2, a2, …, bk, ak, bk+1, bk+2, … bq)
. Продолжая рассуждать аналогичным образом ap+1 ≥ bi1, bi2, … bip. Тогда перестановка с таким множеством максимумов может выглядеть как (b1, a1, b2, a2, …, bk, ak, bk+1, bk+2, … bq)
Тогда для данного множества A проверим, что оно является множеством максимумов такой перестановки. Если это не так, то не существует такой перестановки, что A является ее множеством максимумов.
Как обычно, будем строить перестановку, добавляя в нее элементы, начиная с меньших. В предыдущем пункте мы доказали, что нас интересуют перестановки, вида в которых элементы A и B расположены по возрастанию.
Тогда построенная часть перестановки всегда будет иметь вид . Понятно, что мы никогда не можем поставить два элемента множества A подряд, ведь все элементы, которые мы добавим после будут еще больше.
Состоянием динамики будет количество рассмотренных элементов (i) и длина хвоста из элементов B (j). Считать мы будем количество множеств максимумов перестановки {1, …, i} порядка 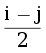 . Перехода вперед есть два, добавить очередной элемент в множество B (тогда он просто ставится в конец перестановки) и добавить очередной элемент в множество A (тогда он ставится после первой буквы B хвоста, то есть, если хвост пуст, то такое множество максимумов недопустимо).
. Перехода вперед есть два, добавить очередной элемент в множество B (тогда он просто ставится в конец перестановки) и добавить очередной элемент в множество A (тогда он ставится после первой буквы B хвоста, то есть, если хвост пуст, то такое множество максимумов недопустимо).
Как теперь восстановить ответ? Нам нужно уметь считать, сколько cуществует множеств максимумов с минимальными элементами {a1, …, ai}. Для этого нужно немного изменить подход к динамике будем считать dp[i][j] — количество способов дополнить большими элементами существующее множество максимов, которое задает конфигурацию (i элементов всего j элементов B в конце). dp[i][j] = dp[i+1][j+1] + dp[i+1][j-1] (второе слагаемое включается только при j > 0).
Как по первым элементам перестановки понять, какую конфигурацию они задают? Очень просто, можно считать ai максимальным элементом, тогда количество способов дополнить такое множество до множества максимумов dp[ai][ai - 2 ⋅ i].
Теперь можно стандартным способом восстанавливать k-е лексикографически множество максимумов, будем добавлять элементы по очереди, на роль каждого элемента пробовать все, начиная с минимально возможного.
Такое решение без длинной арифметики набирало 70 баллов, с длинной арифметикой, в зависимости от оптимальности, 85 или 100.
Задача D: Дорожные войны
Нужно было найти количество полных графов с весами ребер от 1 до M и данным минимальным остовным деревом. Рассмотрим алгоритм Краскала поиска остовного дерева. Он отсортирует все ребра сначала по длине, затем по неупорядоченной паре номеров городов. Далее он будет брать жадно ребра, если после их добавления не образуется цикл.
Для каждого ребра (u,v) найдем минимальный вес, который можем ему назначить. Для этого рассмотрим путь между u и v в дереве и найдем в нем максимальное ребро (x,y) веса w (максимальное сначала по весу, потом по паре вершин). Если ребро (u,v) будет меньше этого ребра, то алгоритм Краскала найдет другой минимальный остов. Тогда, если (u,v) < (x,y) (как неупорядоченные пары), то минимально возможный вес (u,v) равен w0 = w+1, иначе — w0 = w. Тогда количество вариантов стоимости ребра равно M - w0 + 1.
Если хотя бы одно из ограничений не выполняется, то остовное дерево не будет совпадать с данным, иначе — будет. Тогда ответ — произведение количеств вариантов веса по всем ребрам. Такое решение легко превратить в квадратичное.
Но мы рассмотрим независимое квадратичное решение. Отсортируем ребра дерева по весу, затем по паре вершин. Будем добавлять их в дерево по одному. После добавления каждого ребра (u,v) объединяются две компоненты связности. Заметим, что для ребер, соединяющих вершины сливающихся компонент, ребро (u,v) является максимальным на пути. Тогда пусть сливаются компоненты X = {x1, …, xk} и Y = {y1, …, yp}. Давайте посчитаем количество ребер, которые, как пары, меньше (u,v). Пусть их количество равно  . Тогда ответ нужно умножить на
. Тогда ответ нужно умножить на  (первый сомножитель — ребра с нижней границей w+1, второй — ребра с нижней границей w). Для квадратичного решения можно просто перебрать все ребра, соединяющие вершины из X и Y.
(первый сомножитель — ребра с нижней границей w+1, второй — ребра с нижней границей w). Для квадратичного решения можно просто перебрать все ребра, соединяющие вершины из X и Y.
Но давайте более аккуратно поймем, какие пары вершин будут меньше пары (u,v). Будем считать u < v.

Обозначим Xa = {x ∈ X : x < a}; Ya = {y ∈ Y : y < a}. Тогда количество ребер, меньших (u,v) равно (|Xu| ⋅ |Y| + |Yu| ⋅ |X| - |Xu| ⋅ |Yu|) + (|Yv| - |Yu|). В первой скобке мы считаем количество ребер, у которых одна из вершин строго меньше u, а во второй — количество ребер, соединяющих u и вершину, меньшую, чем v, но большую, чем u.
То есть, нам необходима структура, храняшее множество, которая поддерживает слияние двух множеств и может находить количество элементов, меньших данного. Можно использовать для этой цели декартово дерево. Сливать два декартовых дерева можно, добавляя по одному элементы из меньшего дерева в большее (можно показать, что в сумме такие объединения будут работать за 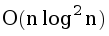 ).
).
Попробуем перенумеровать вершины так, чтобы новые номера вершин компонент на каждом этапе работы алгоритма Крускала, образовывали отрезок. Если мы сможем сделать это, то задача подсчета количества элементов множества, меньших данного числа сводится к подсчету количества чисел на отрезке массива. Такую задачу можно решать оффлайн за 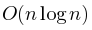 с помощью сканлайна с деревом отрезков.
с помощью сканлайна с деревом отрезков.
Как же перенумеровывать вершины? Давайте рассмотрим все множества, которые возникали в ходе работы алгоритма крускала. Изначально есть n множеств, в каждом из которых по одной вершине. На каждом шаге алгоритма появляется одно новое множество, которое является объединением двух других множеств. Таким образом, можно построить двоичное дерево, вершины которого будут соответствовать множествам. Листам будут соответствовать вершины дерева. Теперь осталось занумеровать листы в порядке обхода дерева.
С помощью того же двоичного дерева множеств можно восстановить отрезки вершин, которые соответствуют множествам. После этого можно запомнить необходимые запросы, выполнить их оффлайн с помощью сканлайна, а затем посчитать ответ.
