Пятый тур
Задача A: Построение булевой схемы
Первое наблюдение: заметим, что у нас всегда есть функции “тождественный верхний вход” и “тождественный нижний вход”.
Пусть мы смогли построить какую-то схему. Посмотрим на тот элемент, который своим выходом соединён с выходом схемы. Его входы — это схемы меньшего размера. Значит, если мы умеем строить все схемы размера не более n элементов, то, перебрав все пары таких схем i и j, а также все доступные элементы k, мы либо получим новую схему из большего количества элементов, либо выясним, что ничего нового получиться не может. Различных типов i, j и k не более 16. Значит, можно просто 16 раз сделать поиск нового элемента за 163 операций (волновой алгоритм, 164).
Вот как делается одна операция. Пусть схема i выдаёт ответ на верхний вход элемента k, а схема j — на нижний вход. Переберём все возможные комбинации (x, y) на входе схемы. Для каждой из четырёх возможных пар (x, y) обозначим сначала за 
выход схемы i и за 
выход схемы 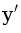j. Теперь применим элемент k ко входам и 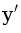; получим значение, которое выдаёт вся схема на входах x и y. Эти четыре значения полностью характеризуют новую схему.
Можно сделать поиск в ширину вместо волнового алгоритма и добиться количества операций 163.
Функции удобно кодировать числами из четырёх битов — какие значения получаются при четырёх возможных вводах.
Какие функции у нас есть — можно кодировать числом из 16 битов.
Входную пару (x, y) можно кодировать одним числом из двух битов.
Задача B: дружелюбные хомячки
Разделяй и властвуй
Поделим точки вертикльной прямой на так, чтобы слева и справа (строго) осталось не более половины точек и посчитаем количество пар, таких, что одна точка слева от этой прямой, а другая — справа (нестрого для второй точки и строго для первой).
Теперь для каждой точки справа определим максимальную верхнюю границу прямоугольника с правым нижним углом в данной точке, такую, что точки из правой половины не попадут в прямоугольник с тамими параметрами.
Для точек левой половины определим минимальную нижнюю границу прямоугольника с левым верхним углом в данной точке, такую, что точки из левой половины не попадут в прямоугольник с такими параметрами.
Точки из разных половин образуют подходящую пару, если верхняя граница правой точки не меньше, чем координата левой и нижняя граница левой не больше, чем координата правой. Тогда каждой точке соответствует отрезок (положение точки, верхняя или нижняя граница). Будем перебирать отрезки в порядке увеличения верхней границы. Будем поддерживать два дерева Фенвика a[i] — количество отрезков левых вершин, с верхней границей i и b[i] — количество отрезков с нижней границей i. A[i] — количество отрезков с верхней границей ≤ i, B[i] — количество отрезков с нижней границей ≤ i. Тогда, встретив отрезок [l,r] (l ≤ r), соответствующий правой вершине, нужно прибавить к ответу B[l] - A[l-1].
Теперь осталось запустить это решение для двух половин. Получили время работы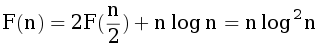 
. Нужно не забыть отразить все точки относительно Ox и запустить решение еще раз.
Сканирующая прямая с деревом отрезков
Зафиксируем горизонтальную прямую и посчитаем для каждой точки на ней количество пустых прямоугольников, таких, что эта точка — правая верхняя. Заметим, что y-координаты подходящих левых нижних точек образуют убывающую последовательность (они должны являться максимумом на суффиксе).
Будем в вершине дерева отрезков поддерживать такие последовательности их можно сливать, в последовательность для вершины войдет последовательность ее левого ребенка и суффикс последовательности правого, такой, что первый элемент на этом суффиксе не больше последнего элемента в последовательности левого ребенка. Границу суффикса можно найти бинарным поиском. Чтобы получить количество точек в последовательности для префикса, нужно перебирать вершины, покрывающие данный префикс, слева-направо и поддерживать текущий последний элемент последовательности.
Задача C: число
Каждое число мы добавим с коэффициентом 2a, где a — количество раз, которое мы выполним операцию умножения на два после добавления данного числа. Тогда можно интерпретировать задачу немного иначе: мы фиксируем максимальный коэффициент, который достигнется (он равен количеству операций умножения на два, которые мы сделаем) и далее выбираем, какие числа с какими коэффициентами мы добавим.
Наблюдение: добавлять число с коэффициентом, болльшим или равным 32 никогда не имеет смысла, потому что 32 добавления одного числа можно заменить на 5 операций умножения на два и одно добавление этого числа.
Теперь давайте считать динамику dp[i][j] — первые i бит числа уже правильно набраны, следующие биты образуют число j. dp[i][j] — минимальное количество прибавлений, с помощью которых можно достичь такого состояния. Из предыдущего соотношения видно, что j ≤ 322. Переходы, при фиксированном i подобны переходам в задаче о рюкзаке, переход от i к i+1 — проверка, что последний бит j совпал с (i+1)-м битом набираемого числа и деление j на два.
Обратите внимание, динамику нужно считать для всех возможных максимальных коэффициентов (на самом деле, достаточно для коэффициентов не меньше log2 x - 10 (x — представляемое число).
Задача D: таблица
Чтобы получить 45 баллов нужно было написать любой разумный перебор.
Чтобы получить 100 баллов нужно было заметить, что корректной таблице можно сопоставить скобочную последовательность из 2N скобок по следующему правилу: поставим открывающие скобки на позиции, соответствующие числам в первой строке таблицы и закрывающие на позиции, соответствующие числам во второй строке таблицы. Такая последовательность действительно будет правильной, ведь баланс на префиксе (разность между количеством открывающих и закрывающих скобок), длины k — это разность, между количеством чисел ≤ k в первой строке таблицы и количеством таких чисел во второй строке. Понятно, что если число во второй строке ≤ k, то и число над ним ≤ k. Тогда количество чисел ≤ k в первой строке не превосходит количество таких чисел во второй.
Обратно из скобочной последовательности получить таблицу можно, выписав в первую строку номера открывающих скобок и во вторую номера закрывающих.
Скобки на позициях из множества A должны быть открывающими, на позициях из множества B должны быть закрывающими, остальные скобки могут быть любыми. Тогда задача сводится к следующей: посчитать количество правильных скобочных последовательностей, соответствующих паттерну вида . Это количество считается стандартной динамикой dp[i][j] — количество скобочных последовательностей длины i с балансом j.