Разбор пятого тура
Задача A
Будем делать бинпоиск по ответу. Научимся проверять, что фиксированный ответ достигается: это значит, что отрезки [ai - x, ai + x] на окружности можно покрыть k точками. Для прямой всё было бы совсем очевидно: ставим точку в правую границу самого левого отрезка (не важно, по какой границы, поскольку они все одной длины) далее находим первый непокрытый отрезок и ставим точку в его правую границу.
На окружности можно делать то же самое, если одна точка зафиксирована, потому что тогда можно удалить все отрезки, покрытые этой точкой, и окружность превратится в прямую. Давайте поймем, как зафиксировать одну точку, перебрав не слишком много разных точек. Во-первый, очевидно, что любая точка покрытия будет являться либо правым либо левым концом какого-нибудь отрезка, во-вторых, на каждом отрезке по определению покрытия должна лежать хотя бы одна точка. Тогда найдем отрезок на котором лежит как можно меньше концов других отрезков. Пусть их количество равно x. Зафиксируем одну из этих точек и будем идти по окружности по часовой стрелке, восстанавливая покрытие.
Чтобы найти следующую точку в покрытии, после точки t найдем самый левый по окружности отрезок, лежащий строго правее t (позиции таких отрезков для всех возможных t можно предподсчитать за O(n)). Тогда понятно, что следующая после t по часовой стрелке точка покрытия — это правая граница найденного отрезка. Заметим, что между t и правой границей не менее x концов отрезков (потому что это минимально возможное количество точек на отрезке). Тогда выбор покрытия для фиксированной первой точки будет работать за 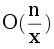 и в итоге мы получим асимптотику
и в итоге мы получим асимптотику 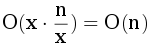 .
.
Задача B
Задача C
Пусть на доске остались два числа a и b. Тогда первое из них — результат операций с числами a1, …, ak, а второе — результат операций с числами ak+1, …, an для некоторого k. Понятно, что каждый из этих результатов нужно максимизировать. Тогда считаем 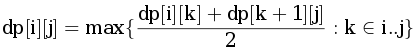 .
.
Задача D
Запросы имеют смысл только если a и b попадают в один и тот же цикл заданной перестановки. Тогда выпишем все циклы в перестановке по порядку x1,1, x1,2, x1,3, …, x1,n1, …, xk,1, …, xk,nk Тогда нам нужна структура, которая умеет на отрезке менять все значения на противоположные и проверять, верно ли, что все значения на отрезке равны нулю (иногда придется делать запрос на двух отрезках). Это умеет дерево отрезков, хранящее в каждой вершине пару 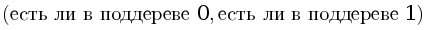 .
.