Разбор первого тура

Задача А: Кинотеатр

Давайте выделим множество точек, которые находятся на расстоянии K от какого-нибудь экрана. Для каждого экрана это будут два отрезка (прямоугольника 1 × x), параллельные экрану на расстоянии K от него. Множество интересующих нас точек — подмножество объединения этих отрезков.

Теперь поймем, какие точки из объединения нас не интересуют. Для каждого экрана множество точек, расстояние от которых до него строго меньше, чем K — это прямоугольник. Все точки, принадлежащие хотя бы одному такому прямоугольнику, точно не входят в ответ.

Понятно, что на самом деле нас интересует разность объединения множества отрезков и множества прямоугольников.

Таким образом, задача свелась к следующей: посчтать площадь разности объединения множества отрезков A и множества прямоугольников B. Можно отдельно решить задачу для вертикальных и горизонтальных отрезков (здесь важно не учесть точки пересечения дважды, то есть, рассматривая вертикальные отрезки, нужно добавить горионтальные в множество B).

Для вертикальных отрезков решим задачу с помощью сканирующей прямой: будем двигать вертикальную прямую в сторону увеличения x и поддерживать дерево отрезков a, a[y] = 1, если точка (x,y) покрыта каким-нибудь прямоугольником из B и a[y] = 0 в противном случае. Тогда для каждого x выделим множество непересекающихся отрезков с таким x и для каждого добавим к ответу 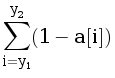(здесь y₁ и y₂ — координаты концов отрезка).

Задача B: Робот в лабиринте

Задачу можно было решать стандартным методом обхода по правилу правой руки. То есть, изначально робот находится в некоторой клетке, он поворачивает направо, пробует пойти вперед, если это удается, то можно вернуться в первоначальное состояние, если нет, робот поворачивается влево и снова пробует пойти вперед, если на этот раз пойти вперед можно, то робот возвращается в первоначальное состояние, если нет, то робот снова поворачивает налево (в итоге робот должен попробовать пойти во всех возможных направлениях, начиная с самого правого.

По такому алгоритму робот будет двигаться вдоль стенки. Из-за того, что лабиринт в задаче является деревом, так можно обойти все клетки.

Задача C: Игра с камнями

Для маленьких n можно было решать задачу с помощью функции гранди 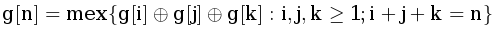По такой формуле все значения g можно посчитать за O(n³). Но, на самом деле, можно заметить, что 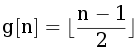и просто делать переход в состояние игры с ненулевой функцией Гранди (выигрышных переходов достаточно много, поэтому можно перебирать их случайно или в каком-нибудь хорошем порядке).

Второй вариант решения — заметить, что из состояния n можно перейти либо в состояние 1, x, x, либо в состояние 2, x, x и далее делать ходы симметричные ходам второго игрока.

Задача D: Подстрока подстроки

Если бы все строки в запросах были одной длины K, то задачу можно было бы решать следующим образом:

• Сохраним для каждого индекса i хэш подстроки s_i, …, s_i+K-1 = h[i]
• Когда приходит запрос [l,r], нужно посчитать количество индексов на отрезке [l, r-K+1], таких, что h[i] = x
• Давайте отсортируем пары (h[i],i).
• Искомое количество индексов — количество пар, лежащих в списке между парами (x,l) и (x,r-K+1) (нестрого)
• Таким образом, на запрос можно ответить с помощью двух бинпоисков

Давайте для длин ≤ C посчитаем массивы h[i] и отсортируем массивы пар (h[i],i), а для запросов длины >C будем решать задачу для каждого запроса за O(|s| + l) с помощью префикс-функции (здесь l — длина строки в запросе). Таким образом, получилось решение за 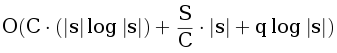. S — суммарная длина строк-запросов.

Можно подобрать C так, чтобы эта величина была достаточно мала.