Разбор третьего тура
Задача A
Если есть хотя бы одно ограничение на то, что строка должна быть периодичной, то подходящих строк довольно мало. Легко понять, что если строка должна быть периодична с периодами a1, a2, …, ak, то это равносильно тому, что она периодична с периодом gcd(a1, …, ak) = g. Тогда всего существует 2g подходящих под эти ограничения строк. Проверить, что заданная строка не периодична с периодом x можно, проверив первые g ⋅ x символов строки.
Если нет ни одного ограничения на периодичность, то можно вывести любую строку, так как ограничения на непереодичность можно опровергать одно за другим в произвольном месте бесконечной строки.
Задача B
В каждый момент времени у уже добавленных вершин дерева есть отрезки контроля, то есть, такие отрезки, что добавленная вершина со значением из отрезка станет сыном вершины, которая контролирует этот отрезок. Первоначально корень дерева контролирует отрезок [0,n-1]. Когда в дерево добавляется вершина со значением x, она становится сыном вершины, контролирующей отрезок [l,r], такой, что l ≤ x ≤ r. Полсле этого новая вершина начинает контролировать отрезки [l,x-1] и [x+1,r], а отрезок [l,r] больше никем не контролируются. Тогда можно поддерживать set текущих отрезков контроля вместе с глубинами контролирующих вершин. Тогда при добавлении можно узнать глубину добавленной вершины и, соответственно, для новых добавляемых отрезков контроля.
Задача C
Можно было применять много стандартных идей в разных комбинациях.
Понятно, что, если буквы без шума, то можно просто посчитать количество белых и черных компонент связности, по этой паре чисел можно восстановить букву.
Чтобы избавиться от шума, можно размыть картинку, то есть, например, для каждой клетки посчитать сумму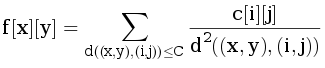 
и установить значение m, после чего считать клетки с f[x][y] ≥ m черными, а остальные — белыми. Константы нужно было подобрать так, чтобы не исчезли никакие дырки в буквах и не склеилась буква <<Ы>>.
Задача D
Будем решать задачу с помощью динамического программирования. Отсортируем туров сначала по координате x, затем по координате y. Будем считать динамику dp[n][minUp][maxDown][minRight][maxRight] — минимальный ответ, если рассмотренно n туров в отсортированном порядке, minUp — минимальная координата y тура, который пошел вверх, maxDown — максимальная координата y тура, который пошел вниз, minRight — минимальная координата y тура, который пошел вправо, maxRight — максимальная координата y тура, который пошел вправо. Переход — поставить очередного тура. При выборе направления тура нужно проверить, что на его пути нет начальных позиций друих туров. Если их нет, то некорректная расстановка может получиться только если путь тура пересекает перпендикулярный ему. С помощью четырех параметров динамики всегда можно понять, нет ли противоречий с предыдущими турами.