Разбор четвертого тура

Лодочный спорт

Сначала решим задачу динамикой за O(NM), где M - это наибольшее из значений b_i.

Пусть d[i][j] - это ответ для первых i школ, если последняя из тех школ, которые послали лодки, послала ровно j. При этом случай, когда никто ничего не послал, тоже учитывается - тогда j=0.

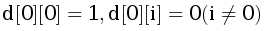Если 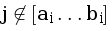(школа i не может послать j лодок), то d[i][j]=d[i-1][j].
Если j ∈ [a_i … b_i] то школа может либо не посылать лодок (тогда это d[i-1][j]), либо послать j лодок (тогда это d[i-1][0]+…+d[i-1][j-1]).

Значит, d[i][j]=d[i-1][0]+…+d[i-1][j].

Ответ на задачу - это d[N][1]+…+d[N][M].

Рассмотрим переход от массива d[i-1] к массиву d[i].

Числа на позициях, не принадлежащих интервалу [a_i … b_i], не меняются.
Число на позиции j ∈ [a_i … b_i] заменяется на префиксную сумму до позиции j включительно.

Возьмём массив d[0] и обработаем N запросов “заменить отрезок на префиксные суммы”.

Разобьём массив на отрезки так, что каждый запрос содержит некоторые отрезки целиком и не содержит куски отрезков. Также выделим элемент 0 в отдельный отрезок. Получится O(N) отрезков.

При выполнении запроса выполним его по-отдельности для каждого из отрезков, которые он покрывает. Сначала заменим на этом отрезке все числа на префиксные суммы (не добавляя при этом сумму чисел до этого отрезка), а затем добавим ко всем элементам сумму чисел до этого отрезка.

Таким образом, нужно реализовать структуру данных, которая поддерживает три операции: добавить во всем элементам число, заменить все элементы на префиксные суммы и посчитать сумму элементов. Каждый отрезок из разбиения будет обрабатываться отдельным экземпляром такой структуры. Всего будет O(N²) запросов.

При этом изначально все отрезки содержат нули, кроме самого первого - к нему следует изначально прибавить 1 (это d[0][0]).

Перейдём к реализации такой структуры.

Предварительно посчитаем массив t[i], i∈[0… N] - это сумма на нём, если сначала применить +1, а затем i раз заменить на префиксные суммы.

Если длина отрезка равна S, то t[i]=C_S+iⁱ⁺¹ (C_n^k - число сочетаний из n по k).

Действительно: после i операций замены на префиксные суммы элементы массива будут элементами столбца номер i треугольника Паскаля в строках с i по i+S-1 (нумерация с нуля). Это легко доказать по индукции. Сумма чисел после i операций - это элемент в строке S+i и в столбце i+1, как показано на рисунке, то есть, t[i]=C_S+iⁱ⁺¹.

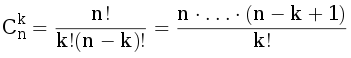, значит, элемент t[i] можно вычислять за O(N) (используя деление по модулю). Всего нужно посчитать O(N) массивов t (по одному в каждом экземпляре структуры), так что их вычисление имеет сложность O(N³).

Перейдём к реализации запросов к структуре.

Будем представлять массив как сумму (поэлементную) нескольких массивов.

Когда мы добавляем x ко всем элементам, мы создаём новый массив из элементов x. Замену на префиксные суммы делаем независимо для всех массивов.

Каждый массив характеризуется двумя числами - x, с которым он был создан, и k - сколько раз он был заменён на префиксные суммы.

То есть, в структуре мы храним пары x_i,k_i. При добавлении числа создаём новую, при замене на префиксные суммы прибавляем 1 ко всем k_i.

Чтобы посчитать сумму, нужно сложить суммы всех массивов - это x_i⋅ t[k_i].

К каждой структуре делается O(N) запросов, поэтому количество пар в каждой структуре - O(N). Всего к структурам делается O(N²) запросов, значит, время работы - O(N³).

Фейерверк

Пусть f_v(x) - это ответ в поддереве вершины v, если мы хотим получить расстояние для всех листьев, равное x. Тогда ответ - это минимум f₁(x).

Будем обходить дерево dfs-ом и находить f_v в каждой вершине. Также будем поддерживать инвариант: f_v - это кусочно-линейная выпуклая функция, коэффициэнты наклона линий целые.

В листе f_v(0)=0, .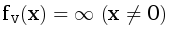

Чтобы найти f_v в промежуточной вершине, нужно: 1. Найти f_v для потомков. 1. Для каждого потомка преобразовать функцию: превратить её из функции на поддереве в функцию на поддереве плюс ребро в него. 1. Сложить полученные функции.

Как добавлять к поддереву v ребро e длины t:

Пусть g(x) - функция, которую мы хотим получить.

Пусть h(x)=|x-t| - сколько стоит изменение ребра e до длины x.

Если мы сделаем расстояние до листьев в поддереве v равным x_v, а длину ребра e равной x_e, то получим расстояние x_v+x_e, потратив f_v(x_v)+h(x_e).

Таким образом, для любых x_v,x_e≥0, g(x_v+x_e)≥ f_v(x_v)+h(x_e).

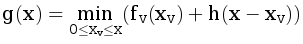График g(x) является суммой Минковского графиков f_v(x) и h(x). Чтобы получить сумму Минковского двух выпуклых кусочно-линейных графиков, нужно:

Взять все отрезки обоих графиков (самый правый кусок считаем отрезком бесконечной длины).
Отсортировать их по угловому коэффициенту.
Соединить их подряд, начиная с точки (0,f_v(0)+h(0))

h(x) представляет собой два куска: один с угловым коэффициэнтом -1 из точки (0,t), второй - с коэффициентом 1 из точки (t,0) в бесконечность.

Пусть f_v достигает минимума на отрезке с x₁ по x₂ (возможно, x₁=x₂).

Находим сумму Минковского:

Отрезки графика f_v(x) при x имеют угловые коэффициенты, меньшие либо равные -1. Поэтому сумма Минковского начнётся с них, при этом они будут сдвинуты вверх на t.
Затем идёт первый отрезок h(x) с коэффициентом -1.
Если 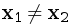, то в f_v(x) есть отрезок с коэффициентом 0. Он будет сейчас.
Затем идёт отрезок h(x) с коэффициентом 1, идущий в бесконечность.
Оставшиеся отрезки f_v(x) имеют коэффициент, больший либо равный единице, поэтому их можно отбросить, так как перед ними был отрезок бесконечной длины.

Заметим, что инвариант, описанный в начале, сохранился: функция осталась выпуклой кусочно-линейной с целыми коэффициентами. При сложении функций он также сохраняется.

Как хранить функцию и быстро применять к ней операции:

Будем хранить отрезки в декартовом дереве.

Чтобы выполнить преобразование, описанное выше, нужно:

Прибавить t к отрезкам с координатами от 0 до x₁ (используя отложенные операции в декартовом дереве).
Отбросить остальные отрезки.
Добавить отрезки с коэффициентами -1, 0, 1 в соответствии с написанным выше.

Как складывать функции:

Пусть нужно сложить f₁ и f₂. Пусть в них соответственно по m₁ и m₂ отрезков, при этом m₁≥ m₂ (другой случай симметричен).

Возьмём каждый из отрезков f₂ и прибавим его к f₁, используя отложенные операции в декартовом дереве. Возможно, при этом придётся разделить какой-то отрезок из f₁. Время работы одного прибавления -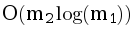

Так как каждый раз меньшая функция прибавляется к большей, общее время работы равно .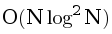

Промежуток

Подзадача 1: не более 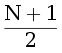запросов.

Сначала сделаем запрос MinMax(0,10¹⁸). Так мы узнаем a₁ и a_N.

Затем сделаем запрос MinMax(a₁+1,a_N-1). Так мы узнаем a₂ и a_N-1.

И так далее: на шаге i мы узнаём a_i и a_N-i+1.

Таким образом, за 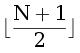запросов мы можем восстановить последовательность. После этого находим ответ.

Подзадача 2: M ≤ 3N.

Сначала сделаем запрос MinMax(0,10¹⁸), потратив на него N+1. Так мы узнаем a₁ и a_N.

Если N=2, то сразу же вернём ответ. Если же N > 2:

Пусть len=a_N-a₁+1 - длина отрезка, который содержит все числа. Если len=N, то сразу же вернём ответ 1. Если же len>N:

Разобьём этот отрезок на N+1 равных частей (его длина как минимум N+1). Если len не делится на N+1, то какие-то части будут больше на 1. Пусть длина каждой части равна z или z+1.

Сделаем запрос MinMax для каждой части. На это мы потратим (N+1) + N = 2N+1. Заметим, что мы уже знаем, что a₁ и a_N входят в крайние части, поэтому при запросе MinMax для них можно исключить из запроса a₁ и a_N. Тогда мы потратим на 2 меньше - 2N-1.

N+1 часть содержит N элементов, поэтому среди них найдётся пустая. Это не может быть крайняя часть, поэтому она находится между какими-либо двумя соседними элементами. Следовательно, ответ как минимум z+1.

Два числа на расстоянии не менее z+1 обязательно находятся в разных частях. Поэтому каждое из двух соседних чисел с наибольшей разностью является крайним в какой-то части. Все такие числа мы нашли, делая запросы MinMax, поэтому можем восстановить ответ.

Всего мы потратим (N+1)+(2N-1)=3N.